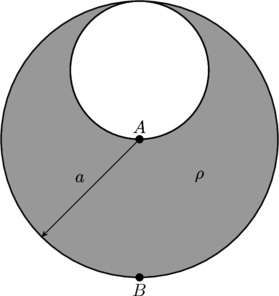
A sphere of radius ![]() is filled with positive charge with uniform density
is filled with positive charge with uniform density ![]() . Then a smaller sphere of radius
. Then a smaller sphere of radius ![]() is carved out, as shown in the figure below, and left empty. What are the direction and magnitude of the electric field at
is carved out, as shown in the figure below, and left empty. What are the direction and magnitude of the electric field at ![]() ? At
? At ![]() ?
?
Related problems:
Electric field in a hollow region
Charge at one corner of a cube
Flux from a charged shell
Solution
This problem can be solved by using the principle of superposition. For instance, consider a point charge ![]() at some point
at some point ![]() in space. It creates an electric field everywhere. However, if you place a …
in space. It creates an electric field everywhere. However, if you place a …