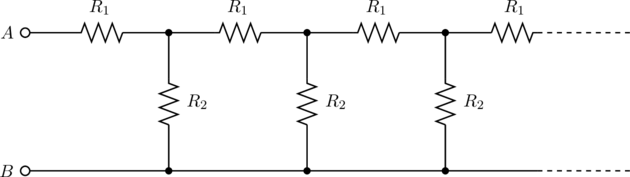
Problem 3.231 from Irodov.
A current ![]() flows along a lengthy straight wire, as shown in the figure below. From the point O the current spreads radially all over an infinite conducting plane perpendicular to the wire. Find the magnetic field above and below the plane.
flows along a lengthy straight wire, as shown in the figure below. From the point O the current spreads radially all over an infinite conducting plane perpendicular to the wire. Find the magnetic field above and below the plane.
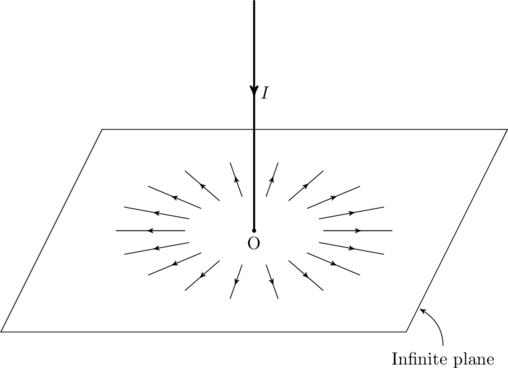
Solution:
We will use this problem to demonstrate the use of Ampere’s law, starting with some simple scenarios. Our goal is to understand …