Simple Harmonic Oscillator

Circular orbit in a harmonic potential

January 21st, 2022jeefirst0 Comments

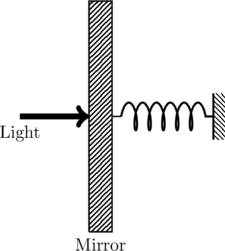
JEE Advanced 2018 Paper 1, Question 1

The potential energy of a particle of mass $m$ at a distance $r$ from a fixed point $O$ is given by $V(r)=k r^{2} / 2$ , where $k$ is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius $R$ about the point $O$ . If $v$ is the speed of the particle and $L$ is the magnitude of its angular momentum about $O$ , which of the following statements is (are) true?

$v=\sqrt{\frac{k}{2 m}} R$
$v=\sqrt{\frac{k}{m}} R$
$L=\sqrt{m k} R^{2}$
$L=\sqrt{\frac{m k}{2}} R^{2}$

Solution

The force due to the given potential is

(1) $\begin{equation*} {\bf F} = -\frac{\partial V}{\partial r} \hat{\bf r} = -k r \hat{\bf r} . \end{equation*}$

The mass also experiences a centrifugal force due to its circular motion,

(2) $\begin{equation*} {\bf F}_{\rm cent} = \frac{m v^2}{r} \hat{\bf r} \end{equation*}$

For the …

Mirror on a spring

January 19th, 2022jeefirst0 Comments

JEE Advanced 2019 Paper 2, Question 12

A perfectly reflecting mirror of mass $M$ mounted on a spring constitutes a spring-mass system of angular frequency $\Omega$ such that $\frac{4 \pi M \Omega}{h} = 10^{24} \, {\rm m}^{-2}$ with $h$ as Planck’s constant. $N$ photons of wavelength $\lambda = 8 \pi \times 10^{-6} \, {\rm m}$ strike the mirror simultaneously at normal incidence such that the mirror gets displaced by $1 \mu{\rm m}$ .
If the value of $N$ is $x \times 10^{12}$ , what is the value of $x$ ?

[Consider the spring as massless]

Rendered by QuickLaTeX.com

Solution

The momentum carried by a single photon is given by the de Broglie relation $p_{\rm ph} = h/\lambda$ . The total momentum carried by $N$ photons is therefore $N \times p_{\rm ph} = Nh/\lambda$ . All the photons hit the mirror simultaneously and are reflected …

Pulleys and masses connected to a spring

January 14th, 2022jeefirst0 Comments

JEE Advanced 2019 Paper 2, Question 2

A block of mass $2 M$ is attached to a massless spring with spring-constant $k$ . This block is connected to two other blocks of masses $M$ and $2 M$ using two massless pulleys and strings. The accelerations of the blocks are $a_{1}, a_{2}$ and $a_{3}$ as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is $x_{0}$ . Which of the following option(s) is/are correct?