Circuits – JEE First

Power dissipated in resistance networks

July 8th, 2022jeefirst0 Comments

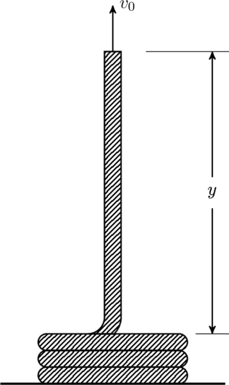
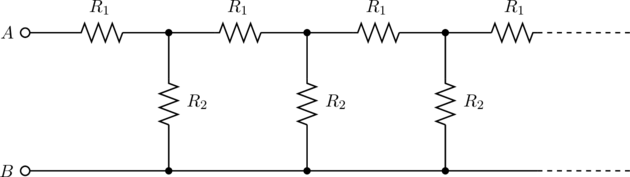
JEE Advanced 2008 Paper 1, Question 25

The figure below shows three resistor configurations R1, R2 and R3 connected to $3 \mathrm{~V}$ battery. If the power dissipated by the configuration R1, R2 and R3 is P1, P2 and P3 respectively, then

Rendered by QuickLaTeX.com

$P1 > P2 > P3$
$P1 > P3 > P2$
$P2 > P1 > P3$
$P3 > P2 > P1$

Solution

The power dissipated by a resistance network is

(1) $\begin{equation*} P = \frac{V^2}{R} . \end{equation*}$

The potential applied to all three networks arre the same, so we just need to find the resistances. Of circuits R2 and R3, the latter has a greater resistance since

(2) $\begin{equation*} % R_3 = 1 \, \Omega + \frac{2 \, \Omega \cdot 2 \, \Omega}{2 \, \Omega + 2 \, \Omega} = 2 \, \Omega , R_3 = 1 \, \Omega + \left( \frac{1}{2 \Omega} + \frac{1}{2 \Omega} \right)^{-1} = 2 \, \Omega , \end{equation*}$

whereas

(3) $\begin{equation*} % R_2 = \frac{1 \, \Omega \cdot 1 \, \Omega}{1 \, \Omega + 1 \, \Omega} = 0.5 \, \Omega . R_2 = \left( \frac{1}{1 \Omega} + \frac{1}{2 \Omega} + \frac{1}{2 \Omega} \right)^{-1} = 0.5 \, \Omega. \end{equation*}$

The first circuit can be redrawn in the following way to make the comparison easier.…

Resistor network with mirror symmetry

February 26th, 2022jeefirst0 Comments

JEE Advanced 2012 Paper 1, Question 12

For the resistance network shown in the figure, choose the correct option(s).

Rendered by QuickLaTeX.com

The current through $PQ$ is zero.
$I_1 = 3$ A.
The potential at $S$ is less than that at $Q$ .
$I_2 = 2$ A.

Solution

We can speed up the solution by noticing the mirror symmetry of the circuit. Let the current $I_1$ split into two parts $I_a$ and $I_b$ at the node $X$ (see figure). Similarly, let the currents going into node $Y$ be $I_a'$ and $I_b'$ . If we were to reverse the polarity of the $12 \, {\rm V}$ battery connected to the circuit, all currents would simply reverse direction, but their magnitudes would remain the …

Terminal velocity in a magnetic field

February 23rd, 2022jeefirst0 Comments

A copper connector of mass $m$ slides down two smooth copper bars, set at an angle $\alpha$ to the horizontal, due to gravity (see figure). At the top the bars are interconnected through a resistance $R$ . The separation between the bars is $\ell$ . The system is located in a uniform magnetic field of induction $B$ , perpendicular to the plane in which the connector slides. The resistance of the bars, the connector and the sliding contacts, as well as the self-inductance of the loop are assumed to be negilible. If the connector is released from rest at $t=0$ ,

Find the velocty $v(t)$ of

…

Missing energy in a rope and a capacitor

February 14th, 2022jeefirst0 Comments

Consider a uniform rope of mass density $\lambda$ coiled on a smooth horizontal table. One end is pulled straight up with a constant speed $v_0$ as shown.

Find the force exerted on the end of the rope as function of the height $y$ .
Compare the power delivered to the rope with the rate of change of the rope’s mechanical energy.

(This is a problem from chapter 5 of Kleppner and Kolenkow)

Rendered by QuickLaTeX.com

To find the force exerted at the top end, note that if we were to pull up a fixed mass with constant velocity $v_0$ , the total force on the mass should …

An infinite ladder of resistors

January 16th, 2022jeefirst0 Comments

Problem 3.152 of Irodov

The figure below shows an inifite circuit formed by the repetition of the same link, consisting of resistance $R_1 = 4.0 \ \Omega$ and $R_2 = 3.0 \ \Omega$ . Find the resistance of this circuit between points $A$ and $B$ .

Rendered by QuickLaTeX.com

Solution

Let’s denote the resistance between the points $A$ and $B$ by $R_{AB}$ . Since the circuit is infinite, removing the first $R_1$ and $R_2$ resistors gives the same arrangement back again — the arrangement is self-similar. That means, the resistance between the points $C$ and $D$ is just $R_{AB}$ without the left-most $R_1$ and $R_2$ resistors, and we may redraw the circuit as shown below.

Rendered by QuickLaTeX.com

It is now straightforward to calculate the resistance,

(1) …