A current ![]() flows along a thin wire, shaped as a regular polygon with
flows along a thin wire, shaped as a regular polygon with ![]() sides, which can be inscribed intro a circle of radius
sides, which can be inscribed intro a circle of radius ![]() . Find the magnetic field at the center of the polygon. What happens if
. Find the magnetic field at the center of the polygon. What happens if ![]() is made very large?
is made very large?
Solution:
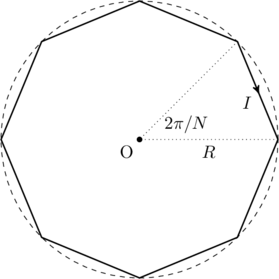
The polygon described in the problem is illustrated in the figure below, for ![]() . The magnetic field created by this structure is the superposition of fields from
. The magnetic field created by this structure is the superposition of fields from ![]() straight current carrying wires of length
straight current carrying wires of length ![]() . Therefore, we will need to find the magnetic field due to a wire of finite length first.
. Therefore, we will need to find the magnetic field due to a wire of finite length first.
The Biot-Savart law gives the magnetic field …

