Spherical gas cloud

JEE Advanced 2019 Paper 1, Question 1

Consider a spherical gas cloud of mass density $\rho(r)$ in free space where $r$ is the radial distance from its center. The gaseous cloud is made of particles of equal mass $m$ moving in circular orbits about the common center with the same kinetic energy $K$ . The force acting on the particles is their mutual gravitational force. If $\rho(r)$ is constant in time, the particle number density $n(r) = \rho(r)/m$ is [ $G$ is the universal gravitational constant]

$\frac{K}{2 \pi r^2 m^2 G}$
$\frac{K}{\pi r^2 m^2 G}$
$\frac{3 K}{\pi r^2 m^2 G}$
$\frac{K}{6 \pi r^2 m^2 G}$

Solution

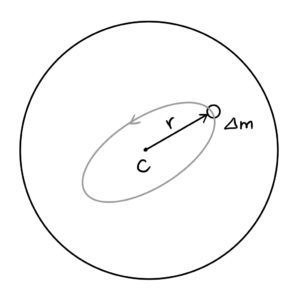
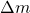A spherical gas cloud of which we consider a small parcel of mass $\Delta m$ moving in a circular orbit (gray) of radius $r$ about the center.

Consider a small parcel of gas in the cloud with mass $\Delta m$ at a distance $r$ from the center of the cloud (see figure). The forces acting on the particle are

The centrifugal force pulling outward:

(1) $\begin{equation*} F_{\rm cent} = \Delta m \cdot \frac{v^2}{r} = \Delta m \cdot \frac{2 K}{m r} \end{equation*}$

where we have inverted the expression for kinetic energy 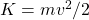$K = m v^2/2$ to write 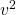$v^2$ in terms of known constants 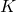$K$ and $m$ .
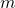The force due to gravity of the spherical cloud of radius $r$ , pulling inward:

(2) $\begin{equation*} F_{\rm grav} = \frac{G}{r^2} \cdot \left( \int_0^r dV' \rho(r') \right) \cdot \Delta m \end{equation*}$

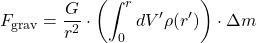
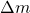Note that the shell outside the region of radius $r$ exerts no force on $\Delta m$ . This is familiar to us from electrostatics, where we know that there is no electric field inside a uniformly charged shell. Both the Coulomb force and Newton’s law of gravitation are inverse square laws and share this property (see discussion below).

We are told that the parcel moves in circular orbits about the center. That means the net force in the radial direction is zero,

(3) $\begin{equation*} F_{\rm cent} - F_{\rm grav} = 0 \end{equation*}$

Substituting (1) and (2) and cancelling $\Delta m$ we get

(4) $\begin{equation*} \frac{G}{r^2} \cdot \int_0^r dV' \rho(r') = \frac{2 K}{m r} \end{equation*}$

Thus, we have arrived at an expression that relates all the variables given in the problem. However, the density $\rho(r')$ is stuck inside an integral. To break it out we need to differentiate.

Since the density only depends on the radial co-ordinate $r'$ we can write

(5) $\begin{equation*} \frac{d}{dr} \left( \int_0^r dV' \rho(r') \right) = \frac{d}{dr} \left( \frac{2 K r}{m G} \right) \end{equation*}$

To simplify the LHS we recall the definition of the derivative of a function $f(r)$ ,

(6) $\begin{equation*} \frac{df(r)}{dr} = \lim_{\Delta r \to 0} \frac{f(r + \Delta r) - f(r)}{\Delta r} \end{equation*}$

which means

(7) $\begin{equation*} \frac{d}{dr} \left( \int_0^r dV' \rho(r') \right) = \lim_{\Delta r \to 0} \frac{1}{\Delta r} \left( \int_0^{r + \Delta r} dV' \rho(r') - \int_0^r dV' \rho(r') \right) . \end{equation*}$

The term in parantheses on the RHS is just the mass of a shell of radius $r$ and small thickness $\Delta r$ with uniform density $\rho(r)$ . That is, $4 \pi {r}^2 \rho(r) \Delta r$ . Therefore\footnote{hello},

(8) $\begin{equation*} \frac{d}{dr} \left( \int_0^r dV' \rho(r') \right) = 4 \pi {r}^2 \rho(r) \end{equation*}$

using the identity $\frac{d}{du} \left( \int_{l}^u f(x) dx \right) = f(u)$ . Subsituting this back into (5) and using $\rho(r) = m \cdot n(r)$ we find

(9) $\begin{equation*} n(r) = \frac{K}{2 \pi m^2 r^2 G} \end{equation*}$

which is option A.

Discussion

Gauss’s Law for gravity: Recall that in electrostatics we determine the field inside a uniformly charged hollow shell using Gauss’s law,

$\oint \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{\rm enclosed}}{\epsilon_0} .$

In a similar way, we have that the surface integral of gravitational force is proportional to the mass enclosed within the surface,

$\oint \mathbf{F}_{\rm grav} \cdot d\mathbf{A} \propto M_{\rm enclosed}.$

We can therefore see that gravitational force inside the shell is zero by the same argument we use to show that electric field $\mathbf{E} = 0$ inside a charged shell.

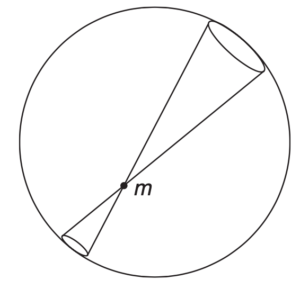
There is another way to see this by a simple argument due to Newton. Consider a thin spherical shell as shown in the figure below. Consider the two small mass elements marked out by a conical surface with its apex at $m$ . The amount of mass in each element is proportional to its surface area. The area increases as (distance) $^2$ . However, the strength of the force varies as 1/(distance) $^2$ , where the distance is measured from the apex to the shell. Thus the forces of the two mass elements are equal and opposite, and cancel. We can pair up all the elements of the shell this way so the total force on $m$ is zero. A thick shell can be regarded as a succession of thin spherical shells, so the force inside is still zero.

Leave a Reply Cancel reply