Particle in a tube

jeefirst0 Comments

JEE Advanced 2019 Paper 2, Question 3

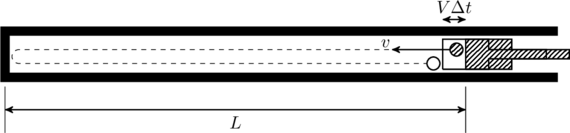
A small particle of mass m moving inside a heavy, hollow and straight tube along the tube axis undergoes elastic collision at two ends. The tube has no friction and it is closed at one end by a flat surface while the other end is fitted with a heavy movable flat piston as shown in figure. When the distance of the piston from the closed end is L=L_{0} the particle speed is v=v_{0} . The piston is moved inward at a very low speed V such that V \ll \frac{{\rm d} L}{L} v_{0}, where {\rm d} L is the infinitesimal displacement of the piston. Which of the following statement(s) is/are correct?

Rendered by QuickLaTeX.com

  1. The rate at which the particle strikes the piston is v / L
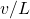
  2. After each collision with the piston, the particle speed increases by 2 V
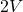
  3. If the piston moves inward by 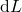{\rm d} L, the particle speed increases by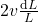 2 v \frac{{\rm d} L}{L}
  4. The particle’s kinetic energy increases by a factor of 4 when the piston is moved inward from 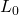L_{0} to \frac{1}{2} L_{0}

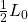
Solution

To find the rate at which the particle strikes the piston, we should first find the time \Delta t between successive collisions. If the particle strikes the piston when it is at a distance L, it gets reflected towards the closed end, reflects and returns to the piston in time \Delta t (see figure below). During this time the piston has moved a distance V \Delta t. So the total time taken for the back and forth journey is

Rendered by QuickLaTeX.com

(1)   \begin{equation*} \Delta t = \frac{L + L - V \Delta t}{v} % = \frac{2L}{v} - \frac{V}{v} \Delta t \implies \Delta t = \frac{1}{1+\frac{V}{v}} \frac{2L}{v} \approx \frac{2L}{v} . \end{equation*}

In the last step we’ve approximated 1+\frac{V}{v} \approx 1 since V \ll v. Therefore, the rate at which the particle strikes the piston is v/2L. So option (A) is incorrect.

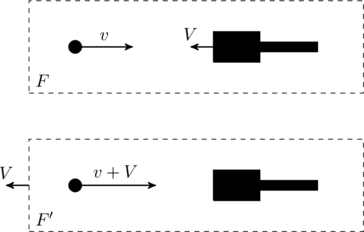
Next, we turn our attention to the increase in velocity of the particle after each collision. We are told that the collision is elastic. In our reference frame F the particle hits moves with a velocity v and the piston has a velocity -V (the minus sign accounts for direction) before collision. If we switch to a frame F' that is also moving at -V the piston will appear to be at rest whereas the particle moves with a velocity v+V. In other words, the piston looks like a stationary wall in F'. The collision will still be elastic, which means, after reflection the particle will have velocty -(v+V) in F'. Translating back to the original frame, we see that the velocity becomes -(v+2V). Therefore, the particle speed does indeed change by 2V after each collision. So option (B) is correct.

Rendered by QuickLaTeX.com

Now that we know the change in speed after each collision, we just need to find the number of collisions in the time it takes the piston to move a distance {\rm d} L. This time is simply {\rm d} L/V, which means there are ({\rm d} L/V)/\Delta t collisions in this interval. The velocity of the particle changes by

(2)   \begin{equation*} {\rm d} v = -\frac{{\rm d} L/V}{2L/v} \times 2 V = -\frac{{\rm d} L}{L} v . \end{equation*}

We have inserted a minus sign by hand to account for the fact that a decrease in L, that is a negative {\rm d} L, will cause an increase in the velocity. It is clear from this expression that option (C) is incorrect, since it is off by a factor of 2.

Finally, we can integrate (2) to find the velocity as a function of L,

(3)   \begin{equation*} \int_{v_0}^{v(L)} \frac{{\rm d} v}{v} = - \int_{L_0}^{L} \frac{{\rm d} L}{L} % \implies % \log \left( \frac{v(L)}{v_0} \right) = \log \left( \frac{L_0}{L} \right) \implies v(L) = \frac{v_0 L_0}{L} . \end{equation*}

Therefore, the velocity at L_0/2 is 2 v_0, which means the kinetic energy indeed becomes 4 times its original value. So option (D) is correct.

Discussion: The ideas from the problem can be used to derive the ideal gas law PV = n R T, as explained in chapter 39 of the Feynman lectures.

Leave a Reply