Insulating spherical shell with a hole

jeefirst0 Comments

JEE Advanced 2019 Paper 1, Question 2.

A thin spherical insulating shell of radius R carries a uniformly distributed charge such that the potential at its surface is V_0. A hole with a small area \alpha 4 \pi R^2 \ (\alpha \ll 1) is made on the shell without affecting the rest of the shell. Which one of the following statements is correct?

  1. The potential at the center of the shell is reduced by 2 \alpha V_0
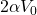
  2. The magnitude of the eletric field at the center of the shell is reduced by \frac{\alpha V_0}{2 R}
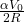
  3. The ratio of the potential at the center of the shell to that of the point at 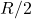R/2 from center towards the hole will be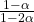 \frac{1-\alpha}{1-2\alpha}
  4. The magnitude of the electric field at a point located on a line passing through the hole and shell’s center, on a distance 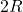2R from the center of the spherical shell will be reduced by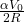 \frac{\alpha V_0}{2 R}

Related problem: A spherical capacitor

Solution:

Prior to making the hole, the electric field inside the shell is zero (Gauss’s law), which means the potential inside the shell is the same as that at the surface, V_0. Now consider the small patch of area \alpha 4 \pi R^2 and the rest of the shell as two separate pieces which combine to form a closed shell. By the principle of superposition the potential or electric field inside the shell is simply the sum of contributions due to each of these pieces,

(1)   \begin{gather*} V_{\rm patch} + V_{\rm rest} = V_0 \\ \mathbf{E}_{\rm patch} + \mathbf{E}_{\rm rest} = 0 . \end{gather*}

If we assume the total charge on the shell is Q, then V_0 = \frac{Q}{4 \pi \epsilon_0 R}. If the patch is sufficiently small it can be treated as a point charge \alpha Q. Therefore, when the patch is removed the potential due to the rest of the shell at its center is

(2)   \begin{equation*} V_{\rm rest} = V_0 - V_{\rm patch} = \frac{Q}{4 \pi \epsilon_0 R} - \frac{\alpha Q}{4 \pi \epsilon_0 R} = V_0(1-\alpha) . \end{equation*}

Therefore, the potential at the center reduces by \alpha V_0. So option (A) is incorrect.

With the patch removed the electric field at the center is

(3)   \begin{equation*} \mathbf{E}_{\rm rest} = - \mathbf{E}_{\rm patch} = - \frac{\alpha Q}{4 \pi \epsilon_0 R^2} (-\hat r) = \frac{\alpha V_0}{R} \hat r \end{equation*}

So option (B) is not correct either.

Following similar arguments that led to (2) we can compute the potential at the center and at R/2 from the center of the shell as

(4)   \begin{gather*} V_{\rm center} = \frac{Q}{4 \pi \epsilon_0 R} - \frac{\alpha Q}{4 \pi \epsilon_0 R} = V_0(1-\alpha) \\ V_{\rm R/2} = \frac{Q}{4 \pi \epsilon_0 R} - \frac{\alpha Q}{4 \pi \epsilon_0 R/2} =V_0(1-2\alpha) \end{gather*}

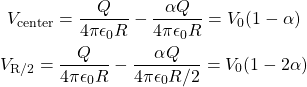
Therefore option (C) is correct.

Let’s check the last option for sake of completeness. The point in question is at a distance 2R from the center of the sphere. But it is only a distance R from the patch that gets removed. Therefore the magnitude of the electric field changes by \frac{\alpha V_0}{R}. So (D) is incorrect.

Leave a Reply