Infinitely bouncing ball

JEE Advanced 2019 Paper 2, Question 9

A ball is thrown from ground at an angle $\theta$ with horizontal and with an initial speed $u_{0}$ . For the resulting projectile motion, the magnitude of average velocity of the ball up to the point when it hits the ground for the first time is $V_{1}$ . After hitting the ground, the ball rebounds at the same angle $\theta$ but with a reduced speed of $u_{0}/\alpha$ . Its motion continues for a long time as shown in figure. If the magnitude of average velocity of the ball for entire duration of motion is $0.8 V_{1}$ , what is the value of $\alpha$ ?

Rendered by QuickLaTeX.com

Solution

The average velocity of the ball between bounces is just the horizontal velocity. Remember, velocity is displacement over time and the net displacement between successive bounces is just the distance covered on the horizontal surface. (The wording ‘average velocity’ confused me when I first read this problem, hence the clarification.)

We also know that the horizontal component of velocity is a constant for projectile motion; up to the first bounce it is just $u_0 \cos \theta$ . So, $V_1 = u_0 \cos \theta$ . Furthermore the ball spends a time $t_1$ in the air before the first bounce, where

(1) $\begin{equation*} u_0 \sin \theta = \frac{g t_1}{2} \implies t_1 = \frac{2 u_0 \sin \theta}{g} . \end{equation*}$

The first equation follows from the fact that the vertical velocity $u_0 \sin \theta$ is deccelerated to $0$ by gravity in the time $t_1/2$ that it takes to reach the peak of the projectile.

Similarly, the average veloctity between the first and second bounce is $V_2 = \frac{u_0}{\alpha} \cos \theta \equiv V_1/\alpha$ and the ball travels for a time $t_2 = \frac{2 u_0 \sin \theta}{\alpha g} = t_1/\alpha$ .
Proceeding in this manner we find that the average velocity between the $(m-1)^{\rm th}$ bounce and the $m^{\rm th}$ one is $V_m = V_1/\alpha^{m-1}$ , and the time of travel is $t_m = t_1/\alpha^{m-1}$ . To find the average velocity, we find the total distance covered by the total time,

(2) $\begin{align*} V_{\rm avg} &= \frac{V_1 t_1 + V_2 t_2 + V_3 t_3 + \dots}{t_1 + t_2 + t_3 + \dots} \nonumber \\ &= \frac{V_1 t_1 \left( 1 + \frac{1}{\alpha^2} + \frac{1}{\alpha^4} + \dots \right)}{t_1 \left( 1 + \frac{1}{\alpha} + \frac{1}{\alpha^2} + \dots \right)} \nonumber \\ &= \frac{V_1 \left( \frac{1}{1-\frac{1}{\alpha^2}} \right)}{\frac{1}{1-\frac{1}{\alpha}}} = \frac{V_1}{1+\frac{1}{\alpha}} . \end{align*}$

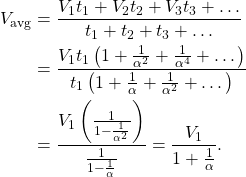
where, in the second to last equality, we’ve used the formula for the sum of an infinite geometric series: $1+r+r^2+r^3+\dots = \frac{1}{1-r}$ , which converges for $r<1$ . We’re told that $V_{\rm avg} = 0.8 V_1$ , and therefore

(3) $\begin{equation*} \frac{1}{1+\frac{1}{\alpha}} = \frac{4}{5} \implies \boxed{\alpha = 4} . \end{equation*}$

Leave a Reply Cancel reply