Heat transferred along two paths

JEE Advanced 2014 Paper 1, Question 20

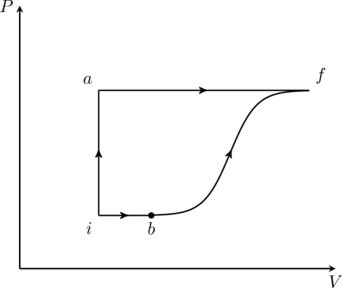
A thermodynamic system is taken from an initial state $i$ with internal energy $U_{i} = 100 \, {\rm J}$ to the final state $f$ along two different paths $i a f$ and $i b f$ , as schematically shown in the figure. The work done by the system along the paths $a f, i b$ and $b f$ are $W_{a f} = 200 \, {\rm J}, W_{i b} = 50 \, {\rm J}$ and $W_{b f} = 100 \, {\rm J}$ respectively. The heat supplied to the system along the path $i a f, i b$ and $b f$ are $Q_{i a f}, Q_{i b}$ and $Q_{b f}$ respectively. If the internal energy of the system in the state $b$ is $U_{b} = 200 \, {\rm J}$ and $Q_{i a f} = 500 \, {\rm J}$ , the ratio $Q_{b f}/Q_{i b}$ is

Rendered by QuickLaTeX.com

Solution

The problem gives us partial information about internal energies, heat transferred, and work done at various points in the PV diagram. We can complete the picture by using the first law of thermodynamics (see note)

(1) $\begin{equation*} \Delta U = \Delta Q - W , \end{equation*}$

where $W$ is the work done by the system. We apply this first to the path $iaf$ . Note that no work is done along $ia$ since volume is constant, therefore $W_{iaf} \equiv W_{af}$ . However, the internal energy at $a$ can be different from that at $b$ (for example, $T \propto P$ for an ideal gas undergoing an isochoric/constant-volume process, which means its internal energy $U(T)$ changes). Thus,

(2) $\begin{equation*} U_f - U_i = Q_{iaf} - W_{af} \implies % U_f = U_i + Q_{iaf} - W_{af} % U_f = 100 \text{ J} + 500 \text{ J} - 200 \text{ J} U_f = 400 \text{ J} . \end{equation*}$

Similarly, along the path $bf$ ,

(3) $\begin{equation*} U_f - U_b = Q_{bf} - W_{bf} \implies Q_{bf} = 300 \text{ J} . \end{equation*}$

Finally, along $ib$

(4) $\begin{equation*} U_b - U_i = Q_{ib} - W_{ib} \implies Q_{ib} = 150 \text{ J} . \end{equation*}$

Therefore, the ratio $Q_{bf}/Q_{ib} = 2$ .

Leave a Reply Cancel reply