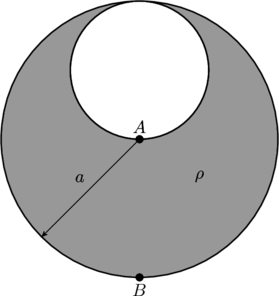
A sphere of radius ![]() is filled with positive charge with uniform density
is filled with positive charge with uniform density ![]() . Then a smaller sphere of radius
. Then a smaller sphere of radius ![]() is carved out, as shown in the figure below, and left empty. What are the direction and magnitude of the electric field at
is carved out, as shown in the figure below, and left empty. What are the direction and magnitude of the electric field at ![]() ? At
? At ![]() ?
?
Related problems:
Electric field in a hollow region
Charge at one corner of a cube
Flux from a charged shell
Solution
This problem can be solved by using the principle of superposition. For instance, consider a point charge ![]() at some point
at some point ![]() in space. It creates an electric field everywhere. However, if you place a negative charge
in space. It creates an electric field everywhere. However, if you place a negative charge ![]() also at
also at ![]() , it exactly cancels the electric field created by the original charge
, it exactly cancels the electric field created by the original charge ![]() . Therefore, it appears that there is no charge anywhere, even though there is in fact a
. Therefore, it appears that there is no charge anywhere, even though there is in fact a ![]() and
and ![]() sitting atop the other one.
sitting atop the other one.
Using this idea, the given charge distribution can be realized as the sum of a cavity-free sphere of radius ![]() and charge density
and charge density ![]() , with another sphere of radius
, with another sphere of radius ![]() with charge
with charge ![]() (note the negative sign).
(note the negative sign).
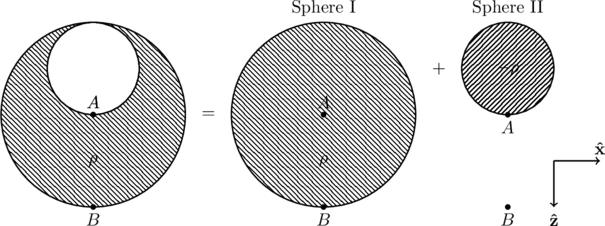
The electric field can now be determined by a simple application of Gauss’s law, since sphere I and sphere II are symmetric objects. Then, the field due to each solid sphere is
(1) 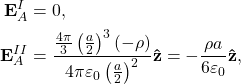
and the net electric field at ![]() is
is
(2) 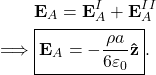
Similarly, for the point ![]()
(3) 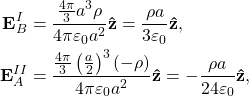
which means the point ![]() experiences a field
experiences a field
(4) 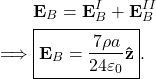
Bonus problem: If a long cylindrical wire of radius ![]() had a portion of radius
had a portion of radius ![]() removed, such that its cross section looks like the figure above, what would be the magnetic field at points
removed, such that its cross section looks like the figure above, what would be the magnetic field at points ![]() and
and ![]() ? Assume that the wire is carrying current of density
? Assume that the wire is carrying current of density ![]() out of the plane of the paper.
out of the plane of the paper.