JEE Advanced 2019 Paper 1, Question 6
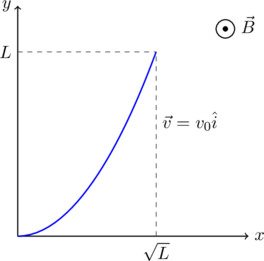
A conducting wire of parabolic shape, initially ![]() , is moving with velocity
, is moving with velocity ![]() in a non-uniform magnetic field
in a non-uniform magnetic field ![]() , as shown in the figure below. If
, as shown in the figure below. If ![]() and
and ![]() are positive constants and
are positive constants and ![]() is the potential difference developed between the ends of the wire, then the correct statement(s) is/are:
is the potential difference developed between the ends of the wire, then the correct statement(s) is/are:
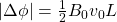 for
for 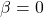 .
. for
for 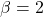 .
.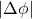 remains the same if the parabolic wire is replaced by a straight wire,
remains the same if the parabolic wire is replaced by a straight wire, 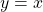 initially, of length
initially, of length 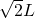 .
.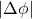 is proportional to the length of the wire projected on the
is proportional to the length of the wire projected on the 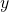 axis.
axis.
Related Problems:
Electromagnetic induction in a twisted loop
Terminal velocity in a magnetic field…