Electricity and Magnetism – Page 3

An infinite ladder of resistors

January 16th, 2022jeefirst0 Comments

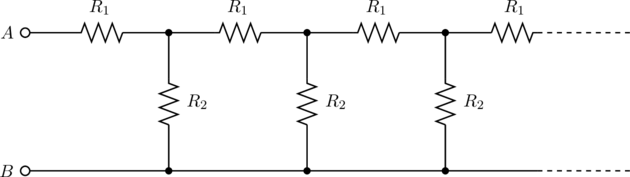
Problem 3.152 of Irodov

The figure below shows an inifite circuit formed by the repetition of the same link, consisting of resistance $R_1 = 4.0 \ \Omega$ and $R_2 = 3.0 \ \Omega$ . Find the resistance of this circuit between points $A$ and $B$ .

Rendered by QuickLaTeX.com

Solution

Let’s denote the resistance between the points $A$ and $B$ by $R_{AB}$ . Since the circuit is infinite, removing the first $R_1$ and $R_2$ resistors gives the same arrangement back again — the arrangement is self-similar. That means, the resistance between the points $C$ and $D$ is just $R_{AB}$ without the left-most $R_1$ and $R_2$ resistors, and we may redraw the circuit as shown below.

Rendered by QuickLaTeX.com

It is now straightforward to calculate the resistance,

(1) …

Electric field in a hollow region

January 9th, 2022jeefirst0 Comments

IIT-JEE 2007 Paper 2, Question 6

(This problem is was repeated in JEE Advanced 2015 Paper 2, Question 11)

A spherical portion has been removed from a solid sphere having a charge distributed uniformly in its volume as shown in the figure. The electric field inside the emptied space is

Rendered by QuickLaTeX.com

zero everywhere
non-zero and uniform
non-uniform
zero only at its center

Solution

As explained in a related problem we can think of the given charge distribution as a …

Charge at one corner of a cube

January 8th, 2022jeefirst0 Comments

A charge $q$ sits at one corner of a cube of side length $a$ as shown in the figure below. What is the electric flux through the shaded side?

Rendered by QuickLaTeX.com

Solution

Since the problem is asking us to find the electric flux it is natural to guess that we need to apply Gauss’s Law. However, we need a closed surface with appropriate symmetry to be able to use Gauss’s Law (see article). So we consider the situation shown below.

Rendered by QuickLaTeX.com

We have placed …

Electric field from a sphere with a cavity

January 8th, 2022jeefirst0 Comments

A sphere of radius $a$ is filled with positive charge with uniform density $\rho$ . Then a smaller sphere of radius $a/2$ is carved out, as shown in the figure below, and left empty. What are the direction and magnitude of the electric field at $A$ ? At $B$ ?

Rendered by QuickLaTeX.com

Solution

This problem can be solved by using the principle of superposition. For instance, consider a point charge $+q$ at some point $P$ in space. It creates an electric field everywhere. However, if you place a …

Flux from a charged shell

December 30th, 2021jeefirst0 Comments

JEE Advanced 2019 Paper 1, Question 8

A charged shell of radius $R$ carries a total charge $Q$ . Given $\Phi$ as the flux of electric field through a closed cylindrical surface of height $h$ , radius $r$
and with its center same as that of the shell. Here, the center of the cylinder is a point on the axis of the cylinder which is equidistant from its top and bottom surfaces. Which of the following option(s) is/are correct?