A copper connector of mass ![]() slides down two smooth copper bars, set at an angle
slides down two smooth copper bars, set at an angle ![]() to the horizontal, due to gravity (see figure). At the top the bars are interconnected through a resistance
to the horizontal, due to gravity (see figure). At the top the bars are interconnected through a resistance ![]() . The separation between the bars is
. The separation between the bars is ![]() . The system is located in a uniform magnetic field of induction
. The system is located in a uniform magnetic field of induction ![]() , perpendicular to the plane in which the connector slides. The resistance of the bars, the connector and the sliding contacts, as well as the self-inductance of the loop are assumed to be negilible. If the connector is released from rest at
, perpendicular to the plane in which the connector slides. The resistance of the bars, the connector and the sliding contacts, as well as the self-inductance of the loop are assumed to be negilible. If the connector is released from rest at ![]() ,
,
- Find the velocty
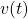 of
of