jeefirst – Page 10

Elongation due to a suspended weight

January 6th, 2022jeefirst0 Comments

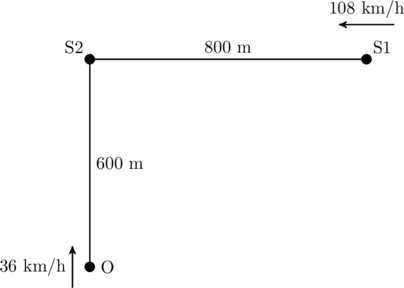
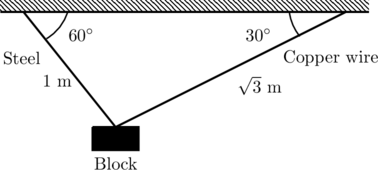
JEE Advanced 2019 Paper 1, Question 14

A block of weight $100$ N is suspended by copper and steel wires of same cross sectional area $0.5$ cm $^2$ and, length $\sqrt{3}$ m and $1$ m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are $30^{\circ}$ and $60^{\circ}$ , respectively.
If elongation in copper wire is $\left(\Delta l_{C}\right)$ and elongation in steel wire is $\left(\Delta l_{S}\right)$ , then the ratio $\frac{\Delta l_{C}}{\Delta l_{S}}$ is

[Young’s modulus for copper and steel are $1 \times 10^{11}$ N/m $^2$ and $2 \times 10^{11}$ N/m $^2$ , respectively.]

Rendered by QuickLaTeX.com

Solution

We will label the tension in the steel and copper wires by $F_S$ and …

Doppler effect and beats

January 6th, 2022jeefirst0 Comments

JEE Advanced 2019 Paper 1, Question 15

A train S1, moving with a uniform velocity of $108$ km/h, approaches another train S2 standing on a platform. An observer O moves with a uniform velocity of $36$ km/h towards S2, as shown in figure. Both the trains are blowing whistles of same frequency $120$ Hz. When $\mathrm{O}$ is $600$ m away from S2 and distance between $\mathrm{S} 1$ and $\mathrm{S} 2$ is $800$ m, what is the number of beats heard by O?

[Speed of the sound $=330$ m/s ]

Rendered by QuickLaTeX.com

Recommended reading: How does Doppler effect work?

Solution

When there is relative motion between the source and observer, the observed frequency $f_o$ is …

Convex lens with two materials

January 2nd, 2022jeefirst0 Comments

JEE Advanced 2019 Paper 1, Question 10

A thin convex lens is made of two materials with refractive indices $n_1$ and $n_2$ as shown in figure. The radius of curvature of the left and right spherical surfaces are equal. $f$ is the focal length of the lens when $n_1 = n_2 = n$ . The focal length is $f + \Delta f$ when $n_1 = n$ and $n_2 = n + \Delta n$ . Assuming $\Delta n \ll (n-1)$ and $1 < n < 2$ , the correct statement(s) is/are,

Rendered by QuickLaTeX.com

$\bigg| \frac{\Delta f}{f} \bigg| < \bigg| \frac{\Delta n}{n} \bigg|$
For $n=1.5, \Delta n = 10^{-3}$ and $f = 20$ cm, the value of $|\Delta f|$ will be 0.02 cm (round off to $2^{\rm nd}$ decimal place).
If $\frac{\Delta n}{n} < 0$ then $\frac{\Delta f}{f} > 0$
The relation between $\frac{\Delta f}{f}$ and $\frac{\Delta n}{n}$ remains unchanged if both the convex surfaces are replaced by concave surfaces of the same radius of curvature.

Related …

Thermodynamic cycle on a VT diagram

January 1st, 2022jeefirst0 Comments

JEE Advanced 2019 Paper 1, Question 9

One mole of a monatomic ideal gas goes through a thermodynamic cycle, as shown in the volume vs. temperature ( $VT$ ) diagram. The correct statement(s) is/are:

[ $R$ is the gas constant]

Rendered by QuickLaTeX.com

Work done in this thermodynamic cycle ( $1 \to 2 \to 3 \to 4 \to 1$ ) is $|W| = \frac{1}{2} R T_0$ .
The above thermodynamic cycle exhibits only isochoric and adiabatic processes.
The ratio of heat transfer during processes $1 \to 2$ and $2 \to 3$ is $\left| \frac{Q_{1 \to 2}}{Q_{2 \to 3}} \right| = \frac{5}{3}$ .
The ratio of heat transfer during processes $1 \to 2$ and $3 \to 4$ is $\left| \frac{Q_{1 \to 2}}{Q_{3 \to 4}} \right| = \frac{1}{2}$ .

Related article: Thermodynamic processes on an ideal gas

Solution

An ideal gas obeys the relations

(1) $\begin{equation*} \text{The ideal gas law: } P V = n R T \end{equation*}$

(2) $\begin{equation*} \text{Work done {\it by} the gas: } W = \int_a^b P dV \end{equation*}$

(3) $\begin{equation*} \text{Internal energy of a monatomic gas: } U = \frac{3}{2} n R T \end{equation*}$

We …

Flux from a charged shell

December 30th, 2021jeefirst0 Comments

JEE Advanced 2019 Paper 1, Question 8

A charged shell of radius $R$ carries a total charge $Q$ . Given $\Phi$ as the flux of electric field through a closed cylindrical surface of height $h$ , radius $r$
and with its center same as that of the shell. Here, the center of the cylinder is a point on the axis of the cylinder which is equidistant from its top and bottom surfaces. Which of the following option(s) is/are correct?