JEE Advanced 2013 Paper 2, Question 20
One mole of a monatomic ideal gas is taken along two cyclic processes ![]() and
and ![]() as shown in the PV diagram. The processes involved are purely isochoric, isobaric, isothermal or adiabatic.
as shown in the PV diagram. The processes involved are purely isochoric, isobaric, isothermal or adiabatic.

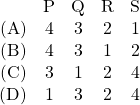
Match the paths in List I with the magnitudes of the work done in List II and select the correct answer using the codes given below the lists.
|
|
|
Codes:
Related Article: Thermodynamic processes on an ideal gas
Solution
Along an isotherm ![]() remains constant whereas
remains constant whereas ![]() is constant for an adiabatic process. Since
is constant for an adiabatic process. Since ![]() we identify the curve
we identify the curve ![]() as an isothermal expansion and
as an isothermal expansion and ![]() as an adiabatic one. The work done by the gas is simply the area under the PV curve. Since
as an adiabatic one. The work done by the gas is simply the area under the PV curve. Since ![]() has the largest area under it, it must match the largest value on the second list,
has the largest area under it, it must match the largest value on the second list, ![]() . That means option (A) should be the answer. We can check explicitly using (9) of our note,
. That means option (A) should be the answer. We can check explicitly using (9) of our note,
(1) ![]()
Only option (A) has this match up, and therefore option (A) is correct, as expected.
For completeness, we will also calculate the work done in th other processes. First, we need to compute the volume at ![]() on the adiabatic curve. Since
on the adiabatic curve. Since ![]() with
with ![]() for a monatomic gas,
for a monatomic gas,
(2) ![]()
The magnitude of work done along ![]() is given by (16) of our note,
is given by (16) of our note,
(3) ![]()
Finally, the work done along the isobaric lines ![]() and
and ![]() are
are
(4) ![]()
Indeed, this confirms that option (A) is correct.