Total internal reflection from a prism

JEE Advanced 2019 Paper 2, Question 11

A monochromatic light is incident from air on a refracting surface of a prism of angle $75^{\circ}$ and refractive index $n_{0}=\sqrt{3}$ . The other refracting surface of the prism is coated by a thin film of material of refractive index $n$ as shown in figure. The light suffers total internal reflection at the coated prism surface for an incidence angle of $\theta \leq 60^{\circ}$ . What is the value of $n^{2}$ ?

Rendered by QuickLaTeX.com

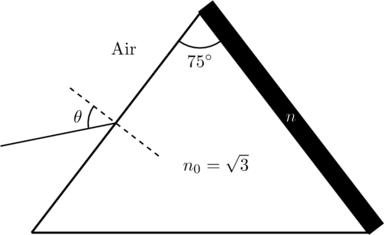
Solution

First we trace the given incident ray through the prism to find the angle at which it is incident on the opposite face (see figure below). For instance, we can extend the normals at each face (the dashed lines) to complete a quadrilateral with vertex $A$ sitting opposite the prism angle $75^\circ$ . But opposite angles of a quadrilateral are supplementary, which means $\angle A + 75^\circ = 180^\circ \implies \angle A = 105^\circ$ .

Rendered by QuickLaTeX.com

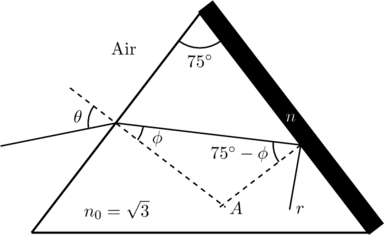
It is then apparent that the angle of incidence at the $n_0$ – $n$ interface is $75^\circ - \phi$ , as indicated. Here $\phi$ is the angle of refraction and it is related to $\theta$ by Snell’s Law,

(1) $\begin{equation*} \sin \theta = n_0 \sin \phi . \end{equation*}$

As $\theta$ is increased, $75^\circ-\phi$ shrinks, till it drops below the critical angle of the $n_0$ – $n$ interface, $\Theta_c = \sin^{-1}(n/n_0)$ . At this point total internal reflection no longer occurs. This is why the problem states that $\theta$ has an upper bound of $60^\circ$ .