A spherical conducting shell with radius ![]() is concentric with a conducting ball with radius
is concentric with a conducting ball with radius ![]() , with
, with ![]() .
.
- Compute the capacitance
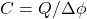 when the shell is grounded and the ball has charge
when the shell is grounded and the ball has charge 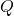 .
. - Compute the capacitance when the ball is grounded and the shell has charge
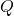 .
. - Compute the full matrix of coefficients of capacitance for the two conductors.
- Considering these conductors as a capacitor, determine its capacitance. That is, assign equal and opposite charges
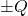 to the shell and the ball, and compute
to the shell and the ball, and compute 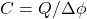 .
.
Related Problem: Insulating spherical shell with a hole
Solution
(a) First, we ground the shell and give the ball a charge ![]() as shown below.
as shown below.
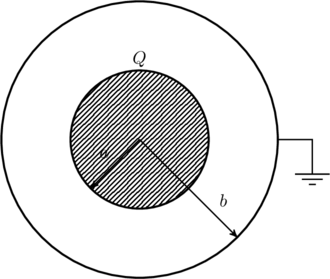
This forces the potential at the shell, ![]() , to be zero. The charge on the ball will create an electric field in the space between the shell and the ball. This creates a potential difference
, to be zero. The charge on the ball will create an electric field in the space between the shell and the ball. This creates a potential difference
(1) ![]()
The capacitance is therefore
(2) ![]()
Check: We can verify the correctness of this expression by making the shell much larger than the ball. That is, we take ![]() and find that
and find that ![]() which is just the capacitance of an isolated conducting sphere in space, as expected.
which is just the capacitance of an isolated conducting sphere in space, as expected.
(b) If the ball is grounded the potential at the surface of the ball will be zero. Since the ball is a perfect conductor there can be no electric field inside it, which means the potential at the surface will be the potential everywhere inside the ball. In other words ![]() (this would also be true if the ball were replaced with a conducting shell). However, we are told that there is a charge
(this would also be true if the ball were replaced with a conducting shell). However, we are told that there is a charge ![]() on the outer shell which tries to make the potential everywhere inside it a constant value of
on the outer shell which tries to make the potential everywhere inside it a constant value of ![]() . To compensate the ball must acquire a charge
. To compensate the ball must acquire a charge ![]() such that
such that
(3) ![]()
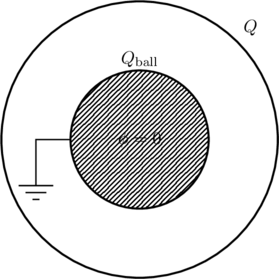
The charge ![]() on the outer shell produces no field inside the shell, as we can see by Gauss’s Law. Therefore, the electric field in the space between the ball and the shell is solely due to
on the outer shell produces no field inside the shell, as we can see by Gauss’s Law. Therefore, the electric field in the space between the ball and the shell is solely due to ![]() ,
,
(4) ![]()
This is the electric field that creates a potential difference between the two conductors. Since ![]() is negative, the field is directed toward the ball, and
is negative, the field is directed toward the ball, and ![]() . Thus,
. Thus,
(5) ![]()
The capacitance is then
(6) ![]()
Check: If we shrink the inner sphere to zero radius, we must recover the capacitance due to an isolated sphere of radius ![]() . Indeed, setting
. Indeed, setting ![]() in the above expression gives
in the above expression gives ![]() .
.
(c) We place a charge ![]() on the shell and
on the shell and ![]() on the ball as stated in the problem. Just like in the previous cases, the field in the region
on the ball as stated in the problem. Just like in the previous cases, the field in the region ![]() is produced by the charge on the ball alone. The ball is at a lower potential, so we find
is produced by the charge on the ball alone. The ball is at a lower potential, so we find
(7) ![]()
Therefore, the capacitance is
(8) ![]()
which is exactly what we found in part (a). But this shouldn’t be surprising — The ball and the conductor together have a net charge of zero, and by Gauss’s Law there is no electric field in the region ![]() . That means the shell is at a potential
. That means the shell is at a potential ![]() , which is the scenario we had in (a).
, which is the scenario we had in (a).
Check: Another interesting limit of (8) is to take ![]() . That is, we make the ball almost as large as the shell and find
. That is, we make the ball almost as large as the shell and find
(9) ![]()
where ![]() is the (small) spacing between the two conductors and
is the (small) spacing between the two conductors and ![]() is the surface area of each conductor when
is the surface area of each conductor when ![]() . Notice that the final expression in (9) is just the capacitance of a parallel plate capacitor. This is because when
. Notice that the final expression in (9) is just the capacitance of a parallel plate capacitor. This is because when ![]() approaches
approaches ![]() the electric field between the ball and the shell is nearly uniform and the arrangement resembles a parallel plate capacitor with plate area
the electric field between the ball and the shell is nearly uniform and the arrangement resembles a parallel plate capacitor with plate area ![]() , with equal and opposite charges on each plate.
, with equal and opposite charges on each plate.
Bonus problem: A capacitor is made of three conducting concentric thin spherical shells of radii ![]() and
and ![]() , with
, with ![]() . The inner and outer spheres are connected by a fine insulated wire passing through a tiny hole in the intermediate sphere. Neglecting the effects of the hole,
. The inner and outer spheres are connected by a fine insulated wire passing through a tiny hole in the intermediate sphere. Neglecting the effects of the hole,
- determine how any net charge
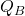 placed on the middle shell distributes itself between its inner and outer surfaces, and
placed on the middle shell distributes itself between its inner and outer surfaces, and - considering these conductors as a capacitor, determine its capacitance.
Tip: Take physical limits of your answer as we did above to check for correctness.