JEE Advanced 2019 Paper 1, Question 18
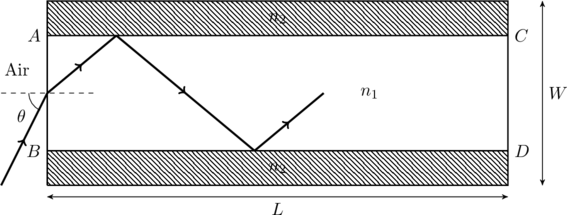
A planar structure of length ![]() and width
and width ![]() is made of two different optical media of refractive indices
is made of two different optical media of refractive indices ![]() and
and ![]() as shown in figure. If
as shown in figure. If ![]() , a ray entering from end
, a ray entering from end ![]() will emerge from end
will emerge from end ![]() only if the total internal reflection condition is met inside the structure. For
only if the total internal reflection condition is met inside the structure. For ![]() m, if the incident angle
m, if the incident angle ![]() is varied, the maximum time taken by a ray to exit the plane
is varied, the maximum time taken by a ray to exit the plane ![]() is
is ![]() s. Determine
s. Determine ![]() .
.
[ Speed of light ![]() m/s. ]
m/s. ]
Solution
To ensure that the ray spends the maximum possible time inside the media, we should arrange it so that the path length of the ray is maximized. We can understand how this is possible by comparing the dashed and solid rays in the figure below. The total length of the dashed path is shorter, which means it takes less time for light to complete its journey along this path. In other words, we want to maximize the number of reflections inside the media ![]() .
.
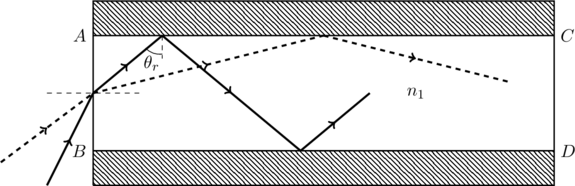
The ray suffers more reflections when the angle of internal reflection ![]() is smaller. But the smallest possible value of this angle is
is smaller. But the smallest possible value of this angle is ![]() , the crtitical angle; there will be no total internal reflection if
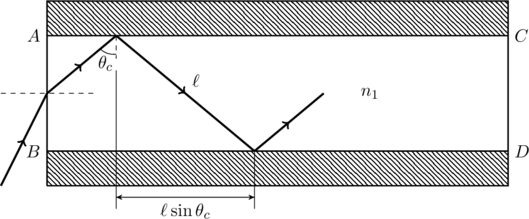
, the crtitical angle; there will be no total internal reflection if ![]() . Furthermore, if we assume the ray travels a distance
. Furthermore, if we assume the ray travels a distance ![]() between each consecutive reflection, the distance traversed along the length of the medium is
between each consecutive reflection, the distance traversed along the length of the medium is ![]() , as shown below. After
, as shown below. After ![]() reflections, the ray covers a total distance
reflections, the ray covers a total distance ![]() along the medium, which means the total length of the path is
along the medium, which means the total length of the path is
(1) ![]()
The velocity of light in the medium is ![]() , therefore the total time taken is
, therefore the total time taken is
(2) ![]()
Plugging in the numbers, we find
(3) ![]()
Notice something interesting about the given values. We have ![]() in the numerator and
in the numerator and ![]() in the denominator. So we can write
in the denominator. So we can write ![]() . This helps make some of the cancellations easier since
. This helps make some of the cancellations easier since ![]() ,
,
(4) ![Rendered by QuickLaTeX.com \begin{gather*} t \times 10^{-9} \ {\rm s} = \frac{9.6 \ {\rm m}}{3 \times 10^{8} \ {\rm m/s}} \times \frac{25}{16} = 50 \times 10^{-9} \ {\rm s} \nonumber \\[1em] \implies \boxed{t=50}. \end{gather*}](https://www.jeefirst.com/wp-content/ql-cache/quicklatex.com-62d270a715f9915591ebd3076ce185bb_l3.png)
Bonus Problem: For what range of the angle of incidence ![]() (see figure) will the ray suffer total internal reflection inside the medium
(see figure) will the ray suffer total internal reflection inside the medium ![]() ?
?