JEE Advanced 2019 Paper 1, Question 14
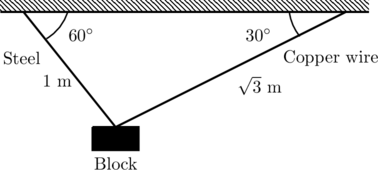
A block of weight ![]() N is suspended by copper and steel wires of same cross sectional area
N is suspended by copper and steel wires of same cross sectional area ![]() cm
cm![]() and, length
and, length ![]() m and
m and ![]() m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are
m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are ![]() and
and ![]() , respectively.
, respectively.
If elongation in copper wire is ![]() and elongation in steel wire is
and elongation in steel wire is ![]() , then the ratio
, then the ratio ![]() is
is
[Young’s modulus for copper and steel are ![]() N/m
N/m![]() and
and ![]() N/m
N/m![]() , respectively.]
, respectively.]
Solution
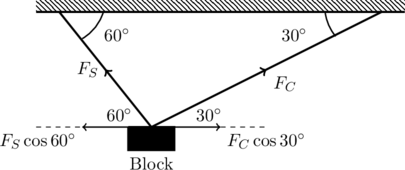
We will label the tension in the steel and copper wires by ![]() and
and ![]() respectively (see figure below). For equilibrium, the horizontal component of the forces must balance each other out. That is,
respectively (see figure below). For equilibrium, the horizontal component of the forces must balance each other out. That is,
(1) ![]()
The Young’s modulus of a material is the ratio of stress (![]() ) to strain (
) to strain (![]() ). That means
). That means
(2) ![]()
where ![]() is the cross-sectional area of the wire, which is the same for both wires in our problem. Thus,
is the cross-sectional area of the wire, which is the same for both wires in our problem. Thus,
(3) ![]()
Notice that we did not have to determine the exact value of the forces at all, only the ratio between the forces.
General tip: In order to save time, find the symbolic expression for the quantity you are asked to calculate, and then figure out what parameters you actually need. The problem might give you more information than you actually require.