February 2022 – JEE First

Resistor network with mirror symmetry

February 26th, 2022jeefirst0 Comments

JEE Advanced 2012 Paper 1, Question 12

For the resistance network shown in the figure, choose the correct option(s).

Rendered by QuickLaTeX.com

The current through 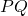$PQ$ is zero.
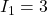$I_1 = 3$ A.
The potential at 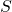$S$ is less than that at $Q$ .
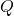$I_2 = 2$ A.

Solution

We can speed up the solution by noticing the mirror symmetry of the circuit. Let the current $I_1$ split into two parts $I_a$ and $I_b$ at the node $X$ (see figure). Similarly, let the currents going into node $Y$ be $I_a'$ and $I_b'$ . If we were to reverse the polarity of the $12 \, {\rm V}$ battery connected to the circuit, all currents would simply reverse direction, but their magnitudes would remain the …

Terminal velocity in a magnetic field

February 23rd, 2022jeefirst0 Comments

A copper connector of mass $m$ slides down two smooth copper bars, set at an angle $\alpha$ to the horizontal, due to gravity (see figure). At the top the bars are interconnected through a resistance $R$ . The separation between the bars is $\ell$ . The system is located in a uniform magnetic field of induction $B$ , perpendicular to the plane in which the connector slides. The resistance of the bars, the connector and the sliding contacts, as well as the self-inductance of the loop are assumed to be negilible. If the connector is released from rest at $t=0$ ,

Find the velocty $v(t)$ of

…

Electromagnetic induction in a twisted loop

February 21st, 2022jeefirst0 Comments

JEE Advanced 2017 Paper 1, Question 5

A circular insulated copper wire loop is twisted to form two loops of area $A$ and $2 A$ as shown in the figure. At the point of crossing the wires remain electrically insulated from each other. The entire loop lies in the plane (of the paper). A uniform magnetic field ${\bf B}$ points into the plane of the paper. At $t=0$ , the loop starts rotating about the common diameter as axis with a constant angular velocity $\omega$ in the magnetic field. Which of the following options is/are correct?

Rendered by QuickLaTeX.com

The emf induced in the loop is proportional to the sum

…

Coriolis effect and angular momentum

February 20th, 2022jeefirst0 Comments

Imagine a mass $m$ moving on the surface of a rotating sphere. For instance, the mass could be parcel of air moving away from a high pressure region in the Earth’s atmosphere. It experiences a Coriolis force which, in the example shown in the figure below, pushes it from its original trajectory (orange) to move eastward (blue). Why does this happen, and how do we understand it intuitively?

Rendered by QuickLaTeX.com

Formally, the Coriolis force on $m$ is given by

(1) $\begin{equation*} {\bf F}_{\rm Coriolis} = - 2 m {\bf \Omega} \times {\bf v}_{\rm rot} , \end{equation*}$

where ${\bf \Omega}$ is the angular velocity of the rotating frame (Earth), and ${\bf v}_{\rm rot}$ is the velocity of $m$ as seen by an observer on the Earth’s …

Missing energy in a rope and a capacitor

February 14th, 2022jeefirst0 Comments

Consider a uniform rope of mass density $\lambda$ coiled on a smooth horizontal table. One end is pulled straight up with a constant speed $v_0$ as shown.

Find the force exerted on the end of the rope as function of the height $y$ .
Compare the power delivered to the rope with the rate of change of the rope’s mechanical energy.

(This is a problem from chapter 5 of Kleppner and Kolenkow)

Rendered by QuickLaTeX.com

To find the force exerted at the top end, note that if we were to pull up a fixed mass with constant velocity $v_0$ , the total force on the mass should …